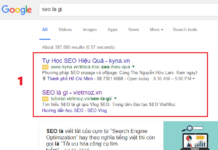
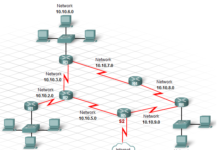
Thuật toán Hợp giải (Robinson) – Hợp giải Robison – là phương pháp chứng minh phản chứng:
Muốn chứng minh 
là đúng, ta Chứng minh điều ngược lại 
là sai
Hợp giải là đúng và đủ cho logic mệnh đề
Để làm rõ vấn đề trên ta đi vào tìm hiểu một số khái niệm sau
HỢP GIẢI MỆNH ĐỀ
Hợp giải mệnh đề là phương pháp suy diễn dựa trên luật hợp giải
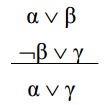
Phát biểu một cách tổng quát, ta có
- Chỉ sử dụng một mình hợp giải mệnh đề (không cần sử dụng các luật khác) có thể xây dựng một chương trình chứng minh lý thuyết đúng và đủ cho tất cả logic mệnh đề
- Mệnh đề kết quả chỉ chứa một bản sao cho mỗi literal. Việc loại bỏ literal trùng gọi là Factoring.
- Đòi hỏi tất cả các câu được chuyển sang dạng hội chuẩn CNF (Conjunctive Normal Form)
DẠNG HỘI CHUẨN CNF
- Biểu thức Dạng hội Chuẩn (CNF) có dạng:
là một mệnh đề
là literal – biến hay phủ định của biến
- Mỗi mệnh đề phải được thoả và có thể được thoả theo nhiều cách
- Mọi câu trong logic mệnh đề đều có thể viết dưới dạng CNF
- Loại bỏ các dấu mũi tên
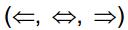bằng định nghĩa - Đưa dấu phủ định vào dùng luật De Morgan
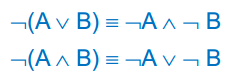
- Phân phối or vào and
- Mọi câu đều có thể được biến đổi thành CNF, nhưng kích thước có thể tăng lên theo lũy thừa.
VÍ DỤ BIẾN ĐỔI CNF
THUẬT GIẢI ROBINSON
- Biến đổi tất cả các câu thành dạng CNF
- Lấy phủ định kết luận, đưa vào KB
- Lặp
- Nếu trong KB có chứa hai mệnh đề phủ định nhau thì trả về false //trả về false => vô lý
- Nếu có hai mệnh đề chứa các literal phủ định nhau thì áp dụng hợp giải.
- Lặp cho đến khi không thể áp dụng tiếp luật hợp giải.
- Trả về true
Một cách phát biểu khác của thuật toán Robinson
–Bước 1: Phát biểu lại giả thiết và kết luận của vấn đề dưới dạng chuẩn như sau:
Trong đó các GTi và KLj được xây dựng từ các biến mệnh đề và các phép toán: 
–Bước 2: Biến đổi dòng trên thành danh sách các mệnh đề:
–Bước 3: Nếu trong danh sách các mệnh đề ở bước 2 có hai mệnh đề đối ngẫu nhau 
thì vấn đề được giải quyết xong, nếu không chuyển sang bước 4.
–Bước 4: Xây dựng một mệnh đề mới bằng cách tuyển một cặp mệnh đề từ danh sách mệnh đề ở bước 2.
Nếu mệnh đề mới có các biến mệnh đề đối ngẫu thì các biến mệnh đề đó được loại bỏ.
-Bước 5: Bổ sung mệnh đề mới vào danh sách và loại bỏ hai mệnh đề cũ vừa tạo thành mệnh đề mới ra khỏi danh sách.
–Bước 6: Nếu không xây dựng thêm mệnh đề mới nào và trong danh sách các mệnh đề không có hai mệnh đề nào đối ngẫu nhau thì vấn đề phát biểu ở dạng chuẩn bước 1 là Sai.
Ví dụ mẫu: Sử dụng thuật toán Robinson, kiểm tra mệnh đề sau:
Hướng dẫn chi tiết:
Bài tập làm thêm:
Câu 1
Cho tập cơ sở tri thức:
Biến đổi tập cơ sở tri thức trên về dạng hội chuẩn và chứng minh G được suy dẫn từ tập cơ sở tri thức trên bằng phương pháp Robinson (DP).
Câu 2
Cho cơ sở tri thức sau:
Biến đổi tập cơ sở tri thức trên về dạng hội chuẩn và chứng minh 
được suy dẫn từ tập cơ sở trên hay không, dùng phương pháp Robinson (DP):
Câu 3
Đặt C(x): “x có một con mèo”, D(x): “x có một con chó”, F(x): “x có một con chồn”.
Biểu diễn các phát biểu sau theo C(x), D(x), F(x), các lượng từ và các phép nối logic. Xét không gian biến là các sinh viên trong lớp
- a) Một sinh viên trong lớp có một con mèo, một con chó hay một con chồn.
- b) Tất cả sinh viên trong lớp có một con mèo, một con chó hay một con chồn.
- c) Một sinh viên nào đó có một con mèo và một con chồn nhưng không có chó.
- d) Không có sinh viên nào trong lớp có một con mèo, một con chó và một con chồn.
- e) Với mỗi loại con vật trên, có một sinh viên trong lớp có một con.
Câu 4
Đặt: L(x): “x là một nhà logic”; C(x): “x uống café”; W(x); “x làm việc chăm chỉ”, T(x):
“x phát biểu định lý”; f(x): hàm trả ra giá trị là bạn của x (giả sử mỗi người có đúng 1 bạn).
Phát biểu các câu sau dưới dạng logic bậc nhất (có sử dụng dấu =):
- Không nhà logic nào uống café
- Bất kỳ ai là một nhà logic cũng đều là bạn của ai đó
- Không người nào phát biểu được định lý lại có một người bạn uống café
- Ai có một người bạn làm việc chăm chỉ thì hoặc là một nhà logic hoặc cũng là một người làm việc chăm chỉ
- Mọi người bạn là một nhà logic
Từ các tiền đề sau:
- Tất cả nhà logic đều uống café.
- Bất kỳ ai không phát biểu được định lý đều không uống café.
- Có một số người mà bạn của họ là nhà logic.
Chứng minh rằng: Có một nhà logic uống café và phát biểu được định lý
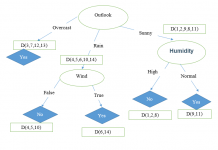
Xem thêm: Ví dụ về thuật toán Quinlan
