Giải thuật Link-state Routing (Định tuyến theo trạng thái đường liên kết) thuộc nhóm các phương thức định tuyến được ứng dụng rộng rãi trong mạng Internet. Link-state Routing ra đời, nhằm mục đích thay thế cho thuật toán Định tuyến theo khoảng cách (Distance Vector Routing), vốn bỏ qua băng thông của đường truyền, xem tất cả các đường truyền có cùng một băng thông như nhau. Đồng thời, Link-state Routing giải quyết được bài toán mất quá nhiều thời gian để hội tụ mà Distance Vector Routing chưa xử lý được.
Giải thuật Link-state Routing mà ta đang nói đến còn được biết đến với cái tên giải thuật Dijkstra – đặt tên theo tên của người phát minh ra nó. Một giải thuật cũng có sự liên quan tương đồng với giải thuật của Dijkstra là giải thuật Prim.
Giải thuật Dijkstra thực hiện tính toán đường dẫn tốn ít chi phí nhất (least-cost path) từ một nút (node) – có thể gọi là nút nguồn, ta minh họa trong bài viết bằng ký hiệu u – đến tất cả các nút khác trong mạng. Giải thuật Dijkstra thực hiện lặp đi lặp lại một số công việc nhất định để sau tất cả, nó có thể tìm ra được k đường dẫn tới tất cả các nút khác trong mạng, mà đồng thời phải đảm bảo k đường dẫn đó sẽ tốn chi phí thấp nhất. Để hiểu rõ thuật toán, ta định nghĩa một số ký hiệu sau:
D(v): chi phí cho đường dẫn hiệu quả nhất từ nút nguồn tới nút đích v sau khi thực hiện việc lặp đi lặp lại các bước giải thuật.
P(v): nút trước (liền kề trước v) trên đường dẫn hiệu quả hiện hành từ nguồn tới v.
N’: Tập hợp một mạng con của các node, v sẽ thuộc N’ nếu đường dẫn tốn ít chi phí nhất từ nguồn tới v đã chắc chắn xác định được.
Giải thuật định tuyến này bao gồm các bước Khởi tạo (Initialization) và các bước Lặp (Loop) theo sau nó. Số lần thực hiện lặp sẽ bằng với số nút có trong mạng. Khi quá trình kết thúc, giải thuật sẽ xác định được các con đường ngắn nhất (The Shortest Paths) từ nút nguồn u tới mỗi nút có trong mạng cho trước.
Minh họa giải thuật trực quan cho nút nguồn u
- Khởi tạo:
- N’={u}
- Với tất cả các nút v
- Nếu v là hàng xóm của u (liền kề và có liên hệ với u, không bị ngắt quãng)
- Thì D(v) = c(u,v)
- Ngược lại D(v) = ∞
- Vòng lặp
- Tìm w không thuộc N’ sao cho D(w) là nhỏ nhất
- Thêm w vào N’
- Cập nhật D(v) cho mỗi hàng xóm v của w và không thuộc N’:
- D(v) = min(D(v), D(w) + c(w,v))
- /* Giá trị mới của v có thể là giá trị cũ ở bước trước của v hoặc là
- giá trị mới bằng giá trị đường dẫn hiệu quả của w cộng với giá trị từ w tới v */
- Cho đến khi N’=N
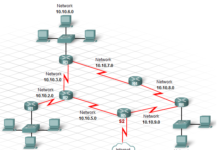
Để dễ dàng hình dung, ta lấy một ví dụ cụ thể được vẽ như hình bên dưới đây. Bằng cách áp dụng thuật toán Dijkstra, ta sẽ tìm ra những đường dẫn hiệu quả nhất từ u tới các nút mạng còn lại.
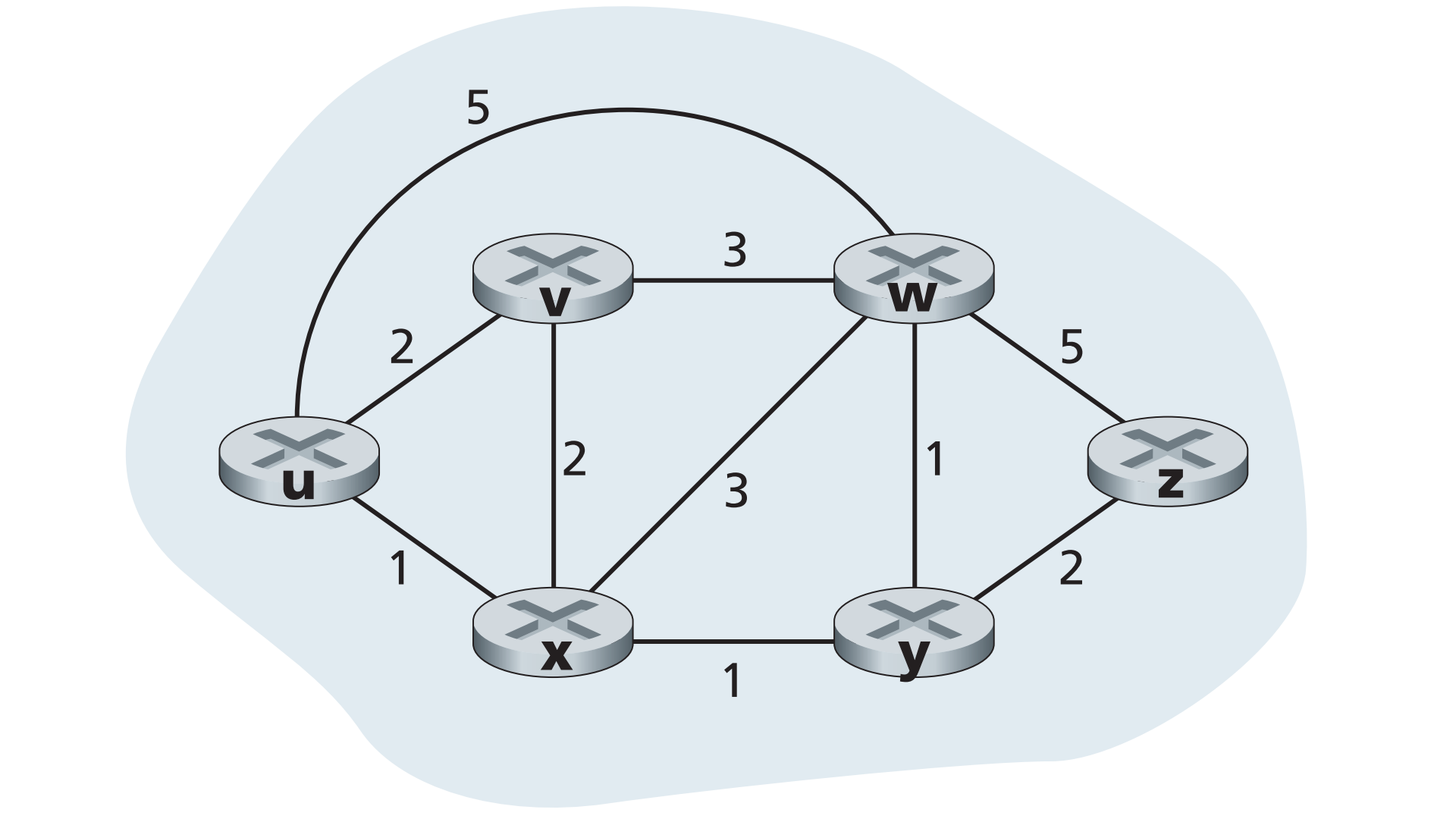
Như đã nói ở phần lý thuyết trên, ta có bao nhiêu nút mạng thì sẽ có bấy nhiêu bước lặp được thực hiện.
Trong phạm vi bài viết, tôi chỉ trình bày một vài bước tiêu biểu, sau đó ta cứ thế thực hiện tiếp tục cho đến khi tìm được nút mạng đích cuối cùng thì dừng.
– Ở bước khởi tạo, ta biết được đường dẫn hiệu quả nhất từ u mà tới thẳng trực tiếp các nút mạng lân cận (hàng xóm của u) nhanh nhất chỉ có thể là v, x và w với các giá trị chi phí khởi tạo ban đầu là 2, 1 và 5. Ở bước này, ta chỉ có thể gán giá trị ∞ cho các chi phí tới y và z vì chúng không có mối liên kết trực tiếp nào tới u.
– Ở bước lặp đầu tiên, ta nhìn tổng quan các các nút mạng chưa được thêm vào N’ và tìm ra trong số đó, nút nào có chi phí thấp nhất từ nó tới u. Nút đó sẽ được thêm vào N’. Cụ thể ở đây, thấy nút đủ điều kiện này không ai khác ngoài x, với mức chi phí là 1 => thêm x và N’. Tới đây, ta sẽ thực hiện công việc như ở dòng 12 trong thuật toán đã giải thích ở trên: tính toán lại các các giá trị cho D(v) của toàn bộ các nút, kết quả sẽ được thể hiện ở bước 1 trong bảng bên dưới đây. Giá trị chi phí của u tới v vẫn không có gì thay đổi. Giá trị của đường dẫn từ u với w (lúc ở bước khởi tạo là 5) thì bây giờ đi qua nút x sẽ có giá trị là 4. Đem giá trị cũ so sánh với giá trị mới tìm rồi lấy kết quả nhỏ nhất – D(v) = min(D(v), D(w) + c(w,v)) – ta sẽ được chi phí hiện tại ở bước đang tính. Tương tự như vậy, tới đây ta sẽ tính được chi phí để tới nút y sẽ bằng 2.
– Tới bước lặp tiếp theo, nút v và y được ghi nhận là có mức chi phí như nhau (đều bằng 2), ta sẽ lựa chọn ngẫu nhiên một trong 2 giá trị đó và thêm nó vào N’ – tôi lấy giá trị y – thì tới đây N’ sẽ có trong nó các giá trị là u, x và y. Các giá trị chi phí phải tính lại đó là các nút v, w và z và để xác định mức phí mới ta cũng làm tương tự như trên, dùng lại công thức ở dòng 12 trong thuật toán.
– Tiếp tục thực hiện sao cho tìm được tất cả các nút trong đề bài và thêm hết vào N’.
VÕ TÌNH THƯƠNG
votinhthuong9@gmail.com
