Giới thiệu về cây quyết định
Trong lý thuyết quyết định (chẳng hạn quản lí rủi ro), một cây quyết định (Decision Tree) là một đồ thị của các quyết định và các hậu quả có thể của nó (bao gồm rủi ro và hao phí tài nguyên). Cây quyết định được sử dụng để xây dựng một kế hoạch nhằm đạt được mục tiêu mong muốn. Các cây quyết định được dùng để hỗ trợ quá trình ra quyết định. Cây quyết định là một dạng đặc biệt của cấu trúc cây.
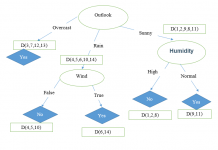
Trong lĩnh vực máy học (Learning Machine), cây quyết định là một kiểu mô hình dự báo (Predictive Model), nghĩa là một ánh xạ từ các quan sát về một sự vật/hiện tượng tới các kết luận về giá trị mục tiêu của sự vật/hiện tượng. Mỗi một nút trong (Internal Node) tương ứng với một biến; đường nối giữa nó với nút con của nó thể hiện một giá trị cụ thể cho biến đó. Mỗi nút lá đại diện cho giá trị dự đoán của biến mục tiêu, cho trước các giá trị của các biến được biểu diễn bởi đường đi từ nút gốc tới nút lá đó. Kỹ thuật máy học dùng trong cây quyết định được gọi là học bằng cây quyết định, hay chỉ gọi với cái tên ngắn gọn là cây quyết định.
Học bằng cây quyết định cũng là một phương pháp thông dụng trong khai phá dữ liệu. Khi đó, cây quyết định mô tả một cấu trúc cây, trong đó, các lá đại diện cho các phân loại còn cành đại diện cho các kết hợp của các thuộc tính dẫn tới phân loại đó. Một cây quyết định có thể được học bằng cách chia tập hợp nguồn thành các tập con dựa theo một kiểm tra giá trị thuộc tính. Quá trình này được lặp lại một cách đệ qui cho mỗi tập con dẫn xuất. Quá trình đệ qui hoàn thành khi không thể tiếp tục thực hiện việc chia tách được nữa, hay khi một phân loại đơn có thể áp dụng cho từng phần tử của tập con dẫn xuất. Một bộ phân loại rừng ngẫu nhiên (Random Forest) sử dụng một số cây quyết định để có thể cải thiện tỉ lệ phân loại.
Cây quyết định cũng là một phương tiện có tính mô tả dành cho việc tính toán các xác suất có điều kiện.
Cây quyết định có thể được mô tả như là sự kết hợp của các kỹ thuật toán học và tính toán nhằm hỗ trợ việc mô tả, phân loại và tổng quát hóa một tập dữ liệu cho trước.
Dữ liệu được cho dưới dạng các bản ghi có dạng:
(x, y) = (x1, x2, x3…, xk, y)
Biến phụ thuộc (Dependant Variable) y là biến mà chúng ta cần tìm hiểu, phân loại hay tổng quát hóa. x1, x2, x3 … là các biến sẽ giúp ta thực hiện công việc đó
Giới thiệu giải thuật ID3
Giải thuật ID3 (gọi tắt là ID3) Được phát triển đồng thời bởi Quinlan trong AI và Breiman, Friedman, Olsen và Stone trong thống kê. ID3 là một giải thuật học đơn giản nhưng tỏ ra thành công trong nhiều lĩnh vực. ID3 là một giải thuật hay vì cách biểu diễn tri thức học được của nó, tiếp cận của nó trong việc quản lý tính phức tạp, heuristic của nó dùng cho việc chọn lựa các khái niệm ứng viên, và tiềm năng của nó đối với việc xử lý dữ liệu nhiễu.
ID3 biểu diễn các khái niệm (concept) ở dạng các cây quyết định (decision tree). Biểu diễn này cho phép chúng ta xác định phân loại của một đối tượng bằng cách kiểm tra các giá trị của nó trên một số thuộc tính nào đó.
Như vậy, nhiệm vụ của giải thuật ID3 là học cây quyết định từ một tập các ví dụ rèn luyện (training example) hay còn gọi là dữ liệu rèn luyện (training data).
Input: Một tập hợp các ví dụ. Mỗi ví dụ bao gồm các thuộc tính mô tả một tình huống, hay một đối tượng nào đó, và một giá trị phân loại của nó.
Output: Cây quyết định có khả năng phân loại đúng đắn các ví dụ trong tập dữ liệu rèn luyện, và hy vọng là phân loại đúng cho cả các ví dụ chưa gặp trong tương lai.
Giải thuật ID3 xây dựng cây quyết định được trình bày như sau:
Lặp:
1. Chọn A <= thuộc tính quyết định “tốt nhất” cho nút kế tiếp
2. Gán A là thuộc tính quyết định cho nút
3. Với mỗi giá trị của A, tạo nhánh con mới của nút
4. Phân loại các mẫu huấn luyện cho các nút lá
5. Nếu các mẫu huấn luyện được phân loại hoàn toàn thì NGƯNG,
Ngược lại, lặp với các nút lá mới.
Thuộc tính tốt nhất ở đây là thuộc tính có entropy trung bình thấp nhất theo thuộc tính kết quả với Entropy được tính như sau:
- Gọi S là tập các mẫu huấn luyện
- Gọi p là tỷ lệ các mẫu dương trong S
- Ta có H ≡ – p.log2p – (1 – p).log2(1 – p)
Entropy trung bình của một thuộc tính bằng trung bình theo tỉ lệ của entropy các nhánh: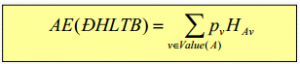 
Tri thức dạng luật
- Tri thức được biểu diễn dưới dạng luật:
IF Điều kiện 1 ^ Điều kiện 2… THEN Kết luận
- Dễ hiểu với con người, được sử dụng chủ yếu trong các
hệ chuyên gia - Rút luật từ cây quyết định: đi từ nút gốc đến nút lá, lấy
các phép thử làm tiền đề và phân loại của nút lá làm kết quả
Lưu ý: Một phiên bản khác của thuật toán ID3 sử dụng Informatic Gain thay cho entropy để chọn thuộc tính quyết định. Công thức tính Informatic Gain như sau:
Gain(A) = Entropy(S) – Entropy(A)
Trong đó: S là tập mẫu và A là một thuộc tính. Entropy(S): độ hỗn loạn của tập S.
Entropy(A): độ hỗn loạn trung bình của thuộc tính A (cách tính như trên)
Xem thêm: Áp dụng giải thuật ID3 vào bài toán dự đoán
