Towers of Hanoi
Nếu bạn đã từng nghe qua thuật toán đệ quy, bạn sẽ thấy thú vị và có phần dễ chịu khi đọc bài này. Nhưng nếu chưa từng nghe qua, thì bây giờ ta bắt đầu.
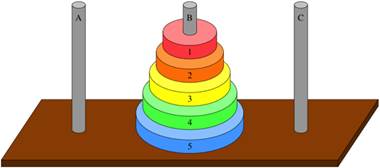
Towers of Hanoi – đây là tên của một thuật toán nổi tiếng ứng dụng tính chất đệ quy. Bạn được cung cấp tổng cộng là 3 cột theo thứ tự A, B và C như hình bên dưới. Và đồng thời, người ta cũng trao cho bạn n đĩa tròn có trục tròn ở giữa có đường kính bằng với đường kính các trụ A, B và C để có thể xếp vào. Và có một lưu ý nhỏ: các đĩa này không bao giờ có hiện tượng 2 đĩa trùng kích thước nhau. Để dễ hình dung, ta đánh số các đĩa từ 1 tới n theo kích thước tăng dần. Vậy suy ra, đĩa nhỏ nhất trong số này luôn luôn là một.
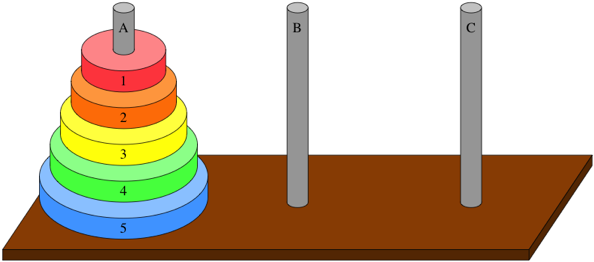
Luật chơi rất đơn giản: ở lần bắt đầu, toàn bộ các đĩa sẽ được xếp chồng vào cột A theo thứ tự nhỏ dần về đỉnh. Để thuận tiện trao đổi hơn nữa, tôi chỉ giới hạn số đĩa trong bài viết này là 5.
Mục tiêu duy nhất của trò chơi này là di chuyển toàn bộ số đĩa đó từ cột A sang cột B và đích đến là cột C. Quá dễ phải không nào? Đưa ra yêu cầu này cho một đứa trẻ năm tuổi thì chắc chắn bé sẽ làm cho ta xem không sai chút yêu cầu nào. Nhưng câu chuyện không hẳn dừng lại ở đây đâu bạn. Đâu có đơn giản đến mức tàn nhẫn như thế được?! Bạn phải bắt buộc tuân theo 2 quy luật sau đây thì mới đúng tính chất của trò Towers of Hanoi:
1. Bạn chỉ được duy chuyển mỗi lần 1 đĩa mà thôi.
2. Không đĩa nào được phép nằm phía trên đĩa nhỏ hơn nó.
Diễn giải ra thử xem nào: Cứ mỗi lần muốn duy chuyển thứ tự vị trí, thì chỉ được nhấc lên 1 đĩa mà thôi? Đúng, chính xác! Không đĩa nào được phép hạ cánh bên trên một đĩa nhỏ con hơn mình? Không còn gì bàn cãi! Đúng hoàn toàn.
Thoạt nhìn, bạn sẽ cho rằng không có gì quá phức tạp cả, dù có thêm 2 quy luật tôi vừa nêu ra. Nhưng nếu thử làm, bạn sẽ thấy không phải cứ nghĩ trong đầu là giải quyết được vấn đề. Nó ứng dụng tính đệ quy ở chỗ bạn phải liên tục di chuyển 1 đĩa bất kỳ với m lần di chuyển về cột A hoặc cột B hay cột C không ràng buộc để cuối cùng đạt được mục tiêu cần có. Và để giải quyết tốt nhất chuyện này, thông thường người ta sẽ chọn một cột làm phần tử trung gian luân chuyển.
Đã có từng một câu chuyện vui liên quan đến thuật toán này. Có một nhà toán học xưa kia đã từng thử giải quyết bài toàn này với 64 đĩa và sau đó ông kết luận: nếu duy chuyển thành công 64 đĩa này từ cột A sang cột B tuân theo quy luật đặt ra, thì lúc đó cũng là lúc thế giới kết thúc!
Vậy, nếu kiên nhẫn và tí xíu giỏi lập luận: bạn sẽ thấy bài toán Towers of Hanoi quả thật không có gì quá khó, nếu đã nắm bắt được quy luật. Nhưng cho dù vậy, cách bạn giải ra đôi khi vẫn chưa tối ưu, dù cho di chuyển thành công toàn bộ đĩa sang cột đích yêu cầu. Tại sao lại như vậy? Đơn giản, số bước thực hiện của bạn quá nhiều. Để loại trừ khả năng bạn chơi theo cách: thử và sai, thử và sai, thử và sai…. thì từ lâu, người ta đã tìm ra quy luật số lần tối ưu cho một số hữu hạn đĩa bất kỳ. Và để tính được con số đó, bạn chỉ việc áp dụng công thức này:
Trong đó, n chính là số đĩa. Đơn cử, với số đĩa là 3, thì số lần duy chuyển các đĩa tối ưu nhất để đạt được mục tiêu yêu cầu là 7. Quay lại vấn đề với 64 đĩa ở trên. Nếu ta áp dụng công thức này, thì số lần thực hiện phải là bao nhiêu? Con số chính xác là 18 446 744 073 709 551 615!
Nếu bạn có cách nào giảm số lần nhỏ hơn 7, hãy trình bày với cộng đồng toán học thế giới, giải Nobel toán học khả năng cao sẽ rơi vào tay bạn! J
Và nếu nói suông như vậy quá trừu tượng, thì bạn có thể hình dung thuật toán tôi đang nói một cách sinh động hơn qua những app games miễn phí trên Google Play. Mặc dù có rất nhiều tác giả viết về thể loại này, nhưng tôi thấy bạn nên bắt đầu với tựa game Swipe The Disk trước là ổn nhất.
https://play.google.com/store/apps/details?id=com.towerofhanoi.Activities
Với games này, nó không yêu cầu bất kỳ quyền truy cập nào với chiếc điện thoại của bạn cả, và đặc biệt là hoàn toàn miễn phí. Và một lưu ý cuối: hãy thử giải bằng cách thực hiện đúng với số lần tối ưu nhé.
Võ T. Thương
