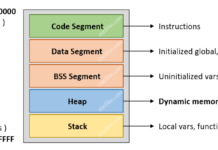
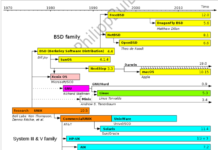
Ý tưởng:
Như đã biết, để sắp xếp một dãy số, ta có thể xét các nghịch thế có trong dãy và triệt tiêu dần chúng đi. Ý tưởng chính của giải thuật là xuất phát từ đầu dãy, tìm tất cả nghịch thế chứa phần tử này, triệt tiêu chúng bằng cách đổi chổ phần tử này với phần tử tương ứng trong cặp nghịch thế. Lặp lại xử lý trên với các phần tử kế tiếp theo trong dãy.
Giải thuật:
Bước 1:
i=0;/ Bắt đầu từ đầu dãy
Bước 2:
j = i+1; // Tìm tất cả các phần tử a[j]<a[i], với j>i
Bước 3:
Trong khi j < N thực hiện
Nếu a[j]<a[i] //xét cặp a[i], a[j]
Swap(a[i],a[j]);
j=j+1;
Bước 4:
i = i+1;
Nếu i<n-1: Lặp lại Bước 2
Ngược lại: Dừng.
Ví dụ:
Cho dãy A gồm 5 phần tử được sắp xếp ngẫu nhiên như sau: 12, 4, 8 , 9, 2.
i=0 ( lấy phần tử a1= 12),
j= i+1; ( lấy phần tử a2= 4),
so sánh: a1 và a2. Do 12 > 4 nên đổi chỗ giữa 12 và 4 ta có được dãy
4, 12, 8, 9, 2.
Tăng j lên: j +1= 2.( lấy phần tử a3 so sánh với a1).
Do 4<8 nên không đổi chỗ a1 và a3.
Tiếp tục tăng j lên 1 đơn vị ta được j=3( lấy phần tử a4 so sánh với a1).
Do 4<9 nên không đổi chỗ a1 và a4.
Tiếp tục tăng j lên 1 đơn vị ta được j=4(lấy phần tử a5 so sánh với a1).
Do 4>2 nên đổi chỗ a1 và a5 ta được dãy mới:
2, 4, 12, 8, 9.
Tiếp tục tăng j lên 1 đơn vị ta được j=5 > N( số phần tử trong mảng) nên dừng lại. Sau đó tăng i lên i lên 1 đơn vị ta được i=2.
j= i +1=3;
So sánh a2 và a3 ta xét thấy: 4<12 nên không cần đổi chỗ.
Tăng j lên 1 đơn vị ta được j=4;
So sánh a2 và a4. Xét thấy 4<8 nên không cần đổi chỗ.
Tăng j lên 1 đơn vị ta được j=5. Tương tự do 4<9 nên không cần đổi chỗ.
Tăng j lên 1 đơn vị: j=6 > N nên dừng lại và tăng i lên 1 ta được i=3.
j=i+1=4;
So sánh a3 và a4.. Xét thấy 12>8 nên đổi chỗ a3 và a4 ta được dãy mới:
2, 4, 8, 12, 9.
Tăng j lên 1 đơn vị ta được j=5. So sánh a3 và a5. Do 8< 9 nên không cần đổi chỗ.
Tăng j lên 1 đơn vị ta được j=6 >N nên dừng và tăng i lên 1 ta được i=4;
j=i+1=5.
So sánh a4 và a5. Xét thấy 12>9 nên đổi chỗ ta được dãy mới:
2, 4, 8, 9, 12.
Tăng j lên 1 đơn vị ta được j=6> N nên dừng lại là tăng i lên 1 ta được i=5. Do i=5=N nên ta dừng thuật toán ở đây và xét thấy dãy cũng đã được sắp xếp hoàn chỉnh.
Trên đây là mô phỏng lại quá trình làm việc của thuật toán InterchangeSort.
Code C/C++
Hàm sắp xếp theo thuật toán InterchangeSort.
void Sapxep(int a[], int n)
{
for (int i = 0; i < n-1;i++)
for (int j = i + 1; j < n;j++)
if (a[i]>a[j])
swap(a[i], a[j]);
}
Hàm đổi chỗ 2 phần tử( Swap).
void swap(int &a, int &b)
{
int x = a;
a = b;
b = x;
}
Hàm main.
void main()
{
int A[100];
NhapMang(A, N);
Sapxep(A, N);
XuatMang(A, N);
getch();
}
Trước khi chạy hàm main các bạn phải có hàm nhập và xuất mảng 1 chiều. Các bạn có thể xem tại đây.
Kết quả:
SO PHAN TU:
4
Phan tu thu 0: 5
Phan tu thu 1: 2
Phan tu thu 2: 3
Phan tu thu 3: 1
Noi dung cua mang la: 1 2 3 5.
Trên đây là một trong những thuật toán sắp xếp của bài toán C/C++. InterchangeSort là một thuật toán rất dễ hiểu và dễ sử dụng nhưng chưa có tính hiệu quả của nó chưa cao. Hẹn gặp lại các bạn ở các thuật toán tiếp theo để giải quyết về tính hiệu quả của các thuật toán sắp xếp. Chúc các bạn thành công.





![[ASP.NET Core MVC] – Hướng dẫn tạo View p3](https://sinhvientot.net/wp-content/uploads/2019/01/Bitmap-MEDIUM_ASP.NET-Core-MVC-Logo_2colors_Square_Boxed_RGB-218x150.png)